ОБРАБОТКА КОСВЕННЫХ ИЗМЕРЕНИЙ

Пусть  u =  f( x, y)  функциональная зависимость между измеряемой величиной u и величинами  x y , ,... , значения которых найдены прямыми измерениями. Действительное значение <u >  определяется как:

 

 

Получим выражение для погрешности  Δu.  Если зафиксировать значения всех аргументов кроме одного, например  x, то приращение функции при изменении ее аргумента имеет вид:

 

 

Если значение Δx мало, то в интервале [<x> - Δx , <x> + Δx ]  функцию u =f (x) можно считать линейной и

 

Величина Δx  u характеризует погрешность Δu, обусловленную погрешностью Δx . Аналогично определяются составляющие погрешности Δu, вносимые другими аргументами. Полная погрешность Δu косвенных измерений u вычисляется либо с помощью квадратичного суммирования либо суммирования по модулю ее составляющих, вносимых каждым аргументом:

 

 

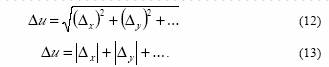
Соотношения (12) применяется в том случае, когда выполняются два условия. Во-первых, погрешность аргументов обусловлена влиянием многих факторов, среди которых нет преобладающего фактора. Во-вторых, погрешности аргументов статистически не связаны.

 В остальных случаях используется соотношение (13). Однако правило суммирования (13) часто приводит к завышенному значению погрешности косвенных измерений. Более подробные сведения о суммирования погрешностей приведены в разделе 8.

 

Пример. Пусть значение сопротивления на участке цепи постоянного тока определяется по результатам прямых измерений тока и напряжения на этом участке. Если погрешность измерения тока и напряжения обусловлены влиянием многих факторов

(температуры, внутренних сопротивлений амперметра и вольтметра, электрических наводок, нестабильности источника питания и др.), то при суммировании погрешностей лучше использовать формулу (12). Если погрешность прямых измерений обусловлена в основном случайным изменением внутреннего сопротивлением источника питания, то лучше применить формулу (13).

Соотношения (9-12) позволяют использовать два алгоритма обработки косвенных измерений. В одном из них необходимо найти аналитические выражения для частных производных, в другом - используются только численные методы.

 

Алгоритм обработки косвенных измерений

1. По известной зависимости измеряемой величины от её аргументов, значения которых найдены с помощью прямых измерений, вычислить действительное значение функции  - формула (9)

2. Вычислить составляющие погрешности как приращения функции по каждому аргументу - формула (10)

или найти частные производные по всем аргументам и вычислить составляющие погрешности -- формула (11)

3. Вычислить полную погрешность функции - формула (12)  формула (13)

4. После округлений результат обработки измерений записать в форме:

 

u=<u> ± Δu,   δ=( Δu/<u>)∙100%,

 

 

(Использовались материалы из Савчук В.П. Обработка результатов измерений. Физическая лаборатория. Ч1:

Учеб. пособие для студентов вузов. — Одесса: ОНПУ, 2002. )